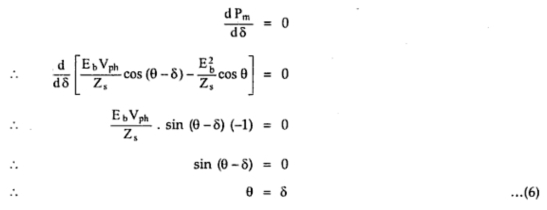SYNCHRONOUS MOTOR Interview Questions With Answer

1.  State the characteristic features of synchronous motor.
Ans:   a.  the motor is not inherently self starting
          b.   The speed of operation is always in synchronous with the supply frequency irrespective of load   conditions
            c.   The motor is capable of operating at any power factor.

2.  In what way synchronous motor is different from other motors?
All dc and ac motors work on the same principle. Synchronous motor operates due to magnetic locking taking place between stator and rotor magnetic fields.
3.  Name any two methods of starting a synchronous motors
•    By an extra 3 phase cage induction motor
•    By providing damper winding in pole phases
•    By operating the pilot excitor as a dc motor
4.  What is the effect on speed if the load is increased on a 3 phase synchronous motor?
The speed of operation remains constant from no load to maximum load in the motor operating at constant frequency bus bars.
5.  Why a synchronous motor is a constant speed motor
 Synchronous motor work on the principle of force developed due to the magnetic attraction established between the rotating magnetic field and the main pole feed. Since the speed of rotating magnetic field is directly proportional to frequency the motor operates at constant speed.
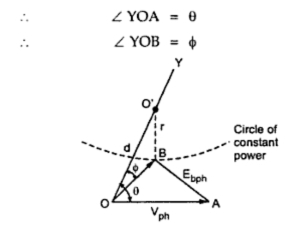
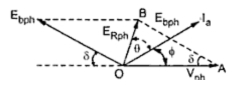
 6. What is the phasor relation between induced emf and terminal voltage of a 3 phase  synchronous motor?The rotating magnetic field is initially established by the prime source of supply V. The main field then causes an emf e to get induced in the 3 phase winding. Hence when the machine operates as a synchronous motor the emf phasor always lags the terminal voltage phasor by the load1torque angle   .
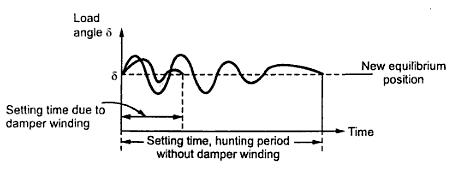
7. At what load angle is power developed in a synchronous motor becomes its maximum value ?
When its load angle   is equal to the impedance angle   .

8. What are V and inverted V curves of synchronous motor ?
The variation of magnitude of line current with respect to the field current is called V curve . The variation of power factor with respect to the field current is called inverted V curve.

9. What happens when the field current of a synchronous motor is increased beyond the normal value at constant input?
Increase in emf causes the motor to have reactive current in the leading direction. The additional leading reactive current causes the magnitude of line current, accompanied by the decrease in power factor.

10.Distinguish between synchronous phase modifier and synchronous condenser

A synchronous motor used to change the power factor or power factor in the supply lines is called synchronous phase modifier.

A synchronous motor operated at no load with over excitation condition to draw large leading reactive current and power is called a synchronous condenser

Synchronous Induction Motor

In the applications where high starting torque and constant speed are desired then synchronous induction motors can be used. It has the advantages of  both synchronous and induction motors. The synchronous motor gives constant speed whereas induction motors can be started against full load torque.

       Consider a normal slip ring induction motor having three phase winding on the rotor as shown in the Fig. 1.

Fig. 1

       The motor is connected to the exciter which gives d.c. supply to the motor through slip rings. One phase carries full d.c. current while the other two carries half of the full d.c. current as they are in parallel. Due to this d.c. excitation, permanent poles (N and S) are formed on the rotor.

       Initially it is run as an slip ring induction motor with the help of starting resistances. When the resistance is cut out the motor runs with a slip. Now the connections are changed and the exciter is connected in series with the rotor windings which will remain in the circuit permanently.

      As the motor is running as induction motor initially high starting torque (upto twice full load value) can be developed. When d.c. excitation is provided it is pulled into synchronism and starts running at constant speed. The synchronous induction motor provides constant speed, large starting torque, low starting current and power factor correction.

       It may be possible that the a.c. winding is put on the rotor and the d.c. excitation is provided on the stator. This simplifies control gear. It also gives better facilities for insulation which permits higher voltages and lower d.c. excitations.

       The d.c. winding must be designed in such a way as to give high m.m.f. with moderate d.c. excitation power. The excitation loss must be distributed evenly over the winding. The mmf distribution should be nearly sinusoidal. It should also provide damping against hunting and it should be satisfactorily started as induction motor.

       When the machine is running as an induction motor there are induced alternating currents in the rotor and it runs below synchronous speed. When the rotor carries d.c. currents in the rotor and it runs below synchronous speed. When the rotor carries d.c. currents the rotor field and hence the rotor must run at synchronous speed. This means that slip must be reduced to zero. But if there is any departure from this speed during normal operation then again induced currents are there in the rotor. The rotor is of low resistance so its windings act as damping winding. Hence no separate damping windings are required.

       When direct current excitation is provided a synchronizing torque is quickly set up. The magnitude of this torque is T_m sinθ where θ is the angle between stator and rotor field. In addition to this induction motor torque is also present which is proportional to the slip (dθ/dt), so long as slip is small. There may also be constant load torque if it is started on load and finally it requires torque J(d²θ/d²t) to accelerate the rotor.

       It can be seen that θ<π as long as the synchronizing torque acts in opposite direction to that of load torque which tends to reduce the angular velocity dθ/dt of the slip motion. when π<θ<2π then synchronizing torque acts in conjuction with load torque to increase the slip i.e. nothing but angular velocity dθ/dt and the motor fails to synchronize.

       As the slip motion is irregular, the motor is subjected to mechanical strains. Also there may be oscillations in current and power factor. Hence it is desired that the motor should synchronize as quickly as possible after switching d.c. excitation. It requires that synchronizing torque should be sufficiently larger than load torque and it should be opposite of load torque. The angle obtained at the instant of switching d.c. excitation also affects pulling into step. Following figures shows oscillograms of rotor current on application of excitation for various values of θ. When the excitation is delayed beyond ₆₀^o it is seen that the rotor fails to synchronize as the induction motor torque and the synchronizing torque work in conjuction and the torque will have pulsating value.

       Thus the motor can be pulled into the synchronism if excitation is applied at a position that the rotor will occupy when both stator and rotor fields are synchronized.

Fig. 2

1.1 Performance Characteristics of Synchronous Induction Motors

       While studying the performance characteristics of synchronous induction motor, three different types of torques are to be considered. These are viz the starting torque which indicates capacity of motor to start against load, pull in torque which indicates the ability of the motor to maintain operation during change over from induction motor to synchronous motor, pull out torque which represents the running of motor synchronously at peak load. The first two torques are closely related with each other and are the characteristics of the machine running as induction motor. The pull out torque is characteristics when it is running running synchronously. The characteristics curves for synchronous induction motor operating at full load unity p.f. and at 0.8 p.f. leading is shown in the Fig. 3.

Fig. 3

       When the load exceeds the synchronous pull out torque, the machine looses synchronism and runs as an induction motor with fluctuation in torque and slip due to d.c. excitation. With reduction in load torque the motor is automatically resynchronized.

1.2 Advantages of Synchronism Induction Motor

       Following are the advantages of synchronous induction motor over salient pole synchronous motor.

i) The synchronous induction motor can start and synchronize against more than full load torque which is not possible with salient pole synchronous motor which must be started against light load.

ii) The exciter required for synchronous induction motor is of smaller capacity as the gap is not long as compared to normal salient pole motor.

iii) The rotor winding in synchronous induction motor can function as providing excitation and required damping. So no separate damper winding is required.

iv) No separate starting and control equipments are required.

1.3 Disadvantages of Synchronous Induction Motor

i) As the gap is small as compared to normal salient pole synchronous motor it will not give large overload capacity.

ii) The variation of power factor is large as compared to normal synchronous motor.
iii) The speed variation is not possible for synchronous induction motor as it runs at constant motor.

1.4 Applications of Synchronous Induction Motor

       The applications where mechanical load is to be driven alongwith phase advancing properties of synchronous motors are to be used then use of synchronous induction motor is better option. Also the applications where in load torque is remaining nearly constant, this motor can be used

Comparison of Synchronous and Induction Motor

Applications of Three Phase Synchronous Motor

The important characteristics of the synchronous motor is its constant speed irrespective of the load conditions, and variable power factor operation. As seen earlier its power factor can be controlled by controlling its excitation. For overexcitation its power factor is leading in nature, which is very important from the power factor correction point of view.

       Due to constant speed characteristics, it is used in machine tools, motor generator sets, synchronous clocks, stroboscopic devices, timing devices, belt driven reciprocating compressors, fans and blowers, centrifugal pumps, vacuum pumps, pulp grinders, textile mills, paper mills line shafts, rolling mills, cement mills etc.

       The synchronous motors are often used as a power factor correction device, phase advancers and phase modifiers for voltage regulation of the transmission lines. This is possible because the excitation of the synchronous motor can be adjusted as per the requirement.

       The disadvantages of synchronous motor are their higher cost, necessity of frequent maintenance and a need of d.c. excitation source, auxiliary device or additional winding provision to make it self starting. Overall their initial cost is very high.

Synchronous Condensers

When synchronous motor is over excited it takes leading p.f. current. If synchronous motor is on no load, where load angle δ is very small and it is over excited (E_b > V) then power factor angle increases almost upto 90^o. And motor runs with almost zero leading power factor condition. This is shown in the phasor diagram Fig. 1.

Fig. 1 Synchronous condenser

       This characteristics is similar to a normal capacitor which takes leading power factor current. Hence over excited synchronous motor operating on no load condition is called as synchronous condenser or synchronous capacitor. This is the property due to which synchronous motor is used as a phase advancer or as power improvement device.

1.1 Disadvantage of Low Power Factor

       In various industries, many machines are of induction motor type. The lighting and heating loads are supplied through transformers. The induction motors and transformers draw lagging current from the supply. Hence the overall power factor is very low and lagging in nature.

       The power is given by,

                       P = VI cosΦ                                         .............. single phase

.^..                     I = P/(VcosΦ)

       The supply voltage is constant and hence for supplying a fixed power P, the current is inversely proportional to the p.f. cosΦ. Let P = KW is to be supplied with a voltage of 230 V then,

Case i) cosΦ = 0.8,

                   I = (5 x10³)/(230 x 0.8) = 27.17 A
Case ii) cos = 0.6,

                   I = (5 x10³)/(230 x 0.6) = 36.23 A

       Thus as p.f. decreases, becomes low, the current drawn from the supply increases to supply same power to the load. But if p.f. maintained high, the current drawn from supply is less.
       The high current due to low p.f. has following disadvantages :

1. For higher current, conductor size required is more which increases the cost.
2. The p.f. is given by
                    cosΦ = Active power/ Apparent = (P in KW)/ (S i.e. KVA rating)

       Thus for fixed active power P, low p.f. demands large KVA rating alternators and transformers. This increases the cost.

3. Large current means more copper losses and poor efficiency.

4. Large current causes large voltage drops in transmission lines, alternators and other equipments. This results into poor regulation. To compensate such drop extra equipments is necessary which further increases the cost.

Note : Hence power factor improvement is must practice. Hence the supply authorities encourage consumers to improve the p.f.

1.1 Use of Synchronous Condenser in Power Factor Improvement

       The low power factor increases the cost of generation, distribution and transmission of the electrical energy. Hence such low power factor needs to be corrected. Such power factor correction is possible by connecting synchronous motor across the supply and operating it on no load with over excitation.

       Now let V_ph is the voltage applied and I_1ph is the current lagging V_ph by angle Φ₁. This power factor Φ₁ is very low, lagging.

       The synchronous motor acting as a synchronous condenser is now connected across the same supply. This draws a leading current of I_2ph.

       The total current drawn from the supply is now phasor of I_ph and I_2ph. This total current I_T now lags V_ph by smaller angle Φ due to which effective power factor gets improved. This is shown in the Fig. 2.

Fig. 2  Power factor correction by synchronous condenser

       This is how the synchronous motor as a synchronous condenser is used to improve power factor of the combined load.

Synchronization With Infinite Bus Bar

There is a specific procedure of connecting synchronous machine to infinite bus bars. Infinite bus bar is one which keeps constant voltage and frequency although load varies. The Fig. 1 shows a synchronous machine which is to be connected to the bus bars with the help of switch K.

        If the synchronous machine is running as a generator then its phase sequence should be some as that of bus bars. The machine speed and field current is adjusted in such a way so as to have the machine voltage same as that of bus bar voltage. The machine frequency should be nearly equal to bus bar frequency so that the machine speed is nearer to synchronous speed.

Fig. 1

        When the above conditions are satisfied, the instant of switching for synchronization should be determined. This can be determined by lamps dark method, Lamps bright and dark method or by using synchroscope.

       Once switch K is closed, the stator and rotor fields of the machine lock into each other and the machine then runs at synchronous speed. The real power exchange with the mains will be now governed by the loading conditions on the shaft while the reactive power exchange will be determined by field excitation.

      The same procedure is to be followed for synchronizing the synchronous motor to the infinite bus bars. The motor is run by an auxiliary device such as small dc or induction motor initially and then synchronized to the bus bars.

       As we know that the synchronous motors are not self starting hence if switch K is closed when rotor is stationary, the average torque will be zero as the two fields run at synchronous speed relative to each other so the motor fails to start. They are made self starting by providing short circuited bars on the rotor which produce torque as produced in case of induction motors.

Hunting in Synchronous Motor

It is seen that, when synchronous motor is on no load, the stator and rotor pole axes almost coincide with each other.

When motor is loaded, the rotor axis falls back with respect to stator. The angle by which rotor retards is called load angle or angle of retardation δ.

       If the load connected to the motor is suddenly changed by a large amount, then rotor tries to retard to take its new equilibrium position.

       But due to inertia of the rotor, it can not achieve its final position instantaneously. While achieving its new position due to inertia it passes beyond its final position corresponding to new load. This will produce more torque than what is demanded. This will try reduce the load angle and rotor swings in other direction. So there is periodic swinging of the rotor on both sides of the new equilibrium position, corresponding to the load. Such a swing is shown in the Fig. 1.

Fig. 1  Hunting in synchronous motor

       Such oscillations of the rotor about its new equilibrium position, due to sudden application or removal of load is called swinging or hunting in synchronous motor.

       Due to such hunting, the load angle changes its value about its final value δ. As changes, for same excitation i.e. E_bph the current drawn by the motor also changes. Hence during hunting there are changes in the current drawn by the motor which may cause problem to the other appliances connected to the same line. The changes in armature current due to hunting is shown in the Fig. 2.

Fig. 2  Current variations during hunting

       If such oscillations continue for longer period, there are large fluctuations in the current. If such variations synchronous with the natural period of oscillation of the rotor, the amplitude of the swing may become so great that motor may come out of synchronism. At this instant mechanical stresses on the rotor are sever and current drawn by the motor is also very large. So motor gets subjected to large mechanical and electrical stresses.

Note : Hence hunting is not desirable phenomenon from motor point of view and must be prevented.

1.1 Use of Damper Winding to Prevent Hunting

       It is mentioned earlier that in the slots provided in the pole faces, a short circuited winding is placed. This is called damper winding.

       When rotor starts oscillating i.e. when hunting starts a relative motion between damper winding and the rotating magnetic field is created. Due to this relative motion, e.m.f. gets induced in the damper winding. According to Lenz's law, the direction of induced e.m.f. is always so as to oppose the cause producing it. The cause is the hunting. So such induced e.m.f. oppose the hunting. The induced e.m.f. tries to damp the oscillations as quickly as possible. Thus hunting is minimised due to damper winding.

       The time required by the rotor to take its final equilibrium position after hunting is called as setting time of the rotor. If the load angle is plotted against time, the schematic representation of hunting can be obtained as shown in the Fig. 3. It is shown in the diagram that due to damper winding the setting time of the rotor reduces considreably.

Fig. Effect of damper winding on hunting

Salient Pole Synchronous Motor

The analysis of salient pole synchronous motor is based on the Blondel's two reaction. The direct and quadrature axis components of current and reactance are same as defined earlier for the synchronous generators. Thus,

                      X_d = Direct axis reactance

                      X_q  = Quadrature axis reactance

                      I_d  = Direct axis component of I_a

                       I_q = Quadrature axis component of I_a

       The complete phasor diagram of lagging p.f. is shown in the Fig. 1.

Fig. 1 Phasor diagram for lagging p.f.

       From the phasor diagram it can be derived that,

Note : For the proof of above results refer example 2.

       The complete phasor diagram of leading p.f. is shown in the Fig. 2.

Fig. 2  Phasor diagram for leading p.f.

       For this leading p.f. case,

Note : Φ should be taken negative for the leading power factor for calculating other parameters.

       While the mechanical power developed per phase is given by,

       Total P_m  = 3 x P_m   

Sponsored links :

Blondel Diagram ( Constant Power Circle) in Synchronous Motor

The Blondel diagram of a synchronous motor is an extension of a simple phasor diagram of a synchronous motor.

       For a synchronous motor, the power input to the motor per phase is given by,

                    P_in  = V_ph I_ph cosΦ                                               ............ per phase

       The gross mechanical power developed per phase will be equal to the difference between  P_in  per phase and the per phase copper losses of the winding.

                   Copper loss per phase = (I_aph)²  R_a

.^..                 P_m   = V_ph I_ph cosΦ - (I_aph)²  R_a                       .......... per phase

       For mathematical convenience let V_ph = V and I_aph = I,

.^..                  P_m   = VI cos - I² R_a

.^..                  I² R_a  - VI cos + P_m  = 0

       Now consider the phasor diagram as shown in the Fig. 1.

Fig. 1

       The equation (1) represents polar equation to a circle. To obtain this circle in a phasor diagram, draw a line OY at an angle θ with respect to OA.

Fig. 2   Blondel diagram

       The circle represented by equation (1) has a centre at some point O' on the line OY. The circle drawn with centre as O' and radius as O'B represents circle of constant power. This is called Blondel diagram, shown in the Fig. 2.

       Thus if excitation is varied while the power is kept constant, then working point B while move along the circle of constant power.

       Let   O'B = Radius of circle = r

       OO' = Distant d

       Applying cosine rule to triangle OBO',

       Now OB represents resultant E_R   which is I_a  Z_s. Thus OB is proportional to current and when referred to OY represents the current in both magnitude and phase.

                             OB = I_a  = I say

       Substituting various values in equation (2) we get,

                              r² = I² + d² - 2dI cosΦ

       Comparing equations (1) and (3) we get,

       Thus the point O' is independent of power P_m  and is a constant for a give motor operating at a fixed applied voltage V.

       Comparing last term of equations (1) and (3),

       The equation shows that as power P_m  must be real, then 4P_m Ra  _≥ V² . The maximum possible power per phase is,

       And the radius of the circle for maximum power is zero. Thus at the time of maximum power, the circles becomes a point O'.

While when the power   P_m   = O, then

                                        r = V/2Ra    = OO'

       This shows that the circle of zero power passes through the points O and A.

       The radius for any power P_m  is given by,

 This is generalised expression for the radius for any power.

Condition for Maximum Power Developed In Synchronous Motor

The value of δ for which the mechanical power developed is maximum can be obtained as,

Note : Thus when R_a is negligible, θ = 90^o for maximum power developed. The corresponding torque is called pull out torque.

1.1 The Value of Maximum Power Developed

       The value of maximum power developed can be obtained by substituting θ =δ in the equation of P_m.

       When R_a is negligible,     θ = 90^o  and cos (θ) = 0 hence,

.^..               R_a = Z_s cosθ   and X_s = Z_s sinθ

       Substituting   cosθ = R_a/Z_s in equation (6b) we get,

        Solving the above quadratic in E_b we get,

       As E_b is completely dependent on excitation, the equation (8) gives the excitation limits for any load for a synchronous motor. If the excitation exceeds this limit, the motor falls out of step.

1.2 Condition for Excitation When Motor Develops (P_m ) R_max

       Let us find excitation condition for maximum power developed. The excitation controls E_b. Hence the condition of excitation can be obtained as,

       Assume load constant hence δ constant.

       but    θ = δ  for P_m = (P_m)_max

         Substitute            cosθ = R_a/Zs

        This is the required condition of excitation.
Note : Note that this is not maximum value of but this is the value of foe which power developed is maximum.
       The corresponding value of maximum power is,

Alternative Expression for Power Developed by a Synchronous Motor

Consider the phasor diagram of a synchronous motor running on leading power factor cosΦ as shown in the Fig. 1.

Fig. 1

       The line CD is drawn at an angle θ to AB.

       The lines AC and DE are perpendicular to CD and AE.

       and angle between AB = E_bph and I_aph is also ψ.

       The mechanical per phase power developed is given by,

       In triangle OBD,

                  BD = OB cosψ = I_a  Zs cosψ

                  OD = OB sin ψ = Ia  Zs sin

       Now    BD = CD - BC = AE - BC

      Substituting in (2),

                   I_a  Zs cosψ = V_ph  cos (θ-δ) - E_b  cosθ

       All values are per phase values

       Substituting (3) in (1),

       This is the expression for the mechanical power developed interms of the load angle δ and the internal machine angle θ, for constant voltage V_ph  and constant E_ph  i.e. excitation.

Power Flow in Synchronous Motor

Net input to the synchronous motor is the three phase input to the stator.

.^..                      P_in = √3 V_L I_L cosΦ W 

       where         V_L = Applied Line Voltage

                          I_L = Line current drawn by the motor

                          cosΦ = operating p.f. of synchronous motor

       or                P_in  = 3 ([er phase power)

                                 = 3 x V_ph I_aph cosΦ W

       Now in stator, due to its resistance R_a per phase there are stator copper losses.
       Total stator copper losses = 3 x (I_aph)² x R_a W

.^..     The remaining power is converted to the mechanical power, called gross mechanical power developed by the motor denoted as P_m.

.^..                P_m = P_in - Stator copper losses
       Now    P = T x ω
.^..                P_m  = T_g  x (2πN_s/60)  as speed is always N_s

       This is the gross mechanical torque developed. In d.c. motor, electrical equivalent of gross mechanical power developed is E_b x I_a, similar in synchronous motor the electrical equivalent of gross mechanical power developed is given by,

                           P_m = 3 E_bph x I_aph x cos (E_bph ^ I_aph)
i) For lagging p.f.,
            E_bph ^ I_aph = Φ - δ
ii) For leading p.f.,
             E_bph ^ I_aph = Φ + δ
iii) For unity p.f.,
              E_bph ^ I_aph  = δ

Note : While calculating angle between E_bph and I_aph from phasor diagram, it is necessary to reverse E_bph phasor. After reversing E_bph, as it is in opposition to V_ph, angle between E_bph and I_aph must be determined.

       In general,

       Positive sign for leading p.f.
       Neglecting sign for lagging p.f.

       Net output of the motor then can be obtained by subtracting friction and windage i.e. mechanical losses from gross mechanical power developed.

.^..                      P_out = P_m - mechanical losses.

       where         T_shaft = Shaft torque available to load.
                          P_out = Power available to load
.^..     Overall efficiency = P_out/P_in

Expression for Back E.M.F or Induced E.M.F. per Phase in S.M.

Case i) Under excitation, E_bph < V_ph .

       Z_s = R_a + j X_s = | Z_s |  ∟θ Ω

       θ = tan^-1(X_s/R_a)

       E_Rph  ^ I_aph = θ, I_a lags always by angle θ.

       V_ph = Phase voltage applied

       E_Rph = Back e.m.f. induced per phase

       E_Rph = I_a x Z_s V            ... per phase

       Let p.f. be cosΦ, lagging as under excited,

       V_ph  ^ I_aph = Φ

       Phasor diagram is shown in the Fig. 1.

Fig. 1 Phasor diagram for under excited condition

       Applying cosine rule to Δ OAB, 

       (E_bph)² = (V_ph)² + (E_Rph)² - 2V_ph E_Rph x (V_ph ^ E_Rph)

       but V_ph ^ E_Rph = x = θ - Φ

       (E_bph)² = (V_ph)² + (E_Rph)² - 2V_ph E_Rph x (θ - Φ)                   ......(1)

       where E_Rph =  I_aph x Z_s

       Applying sine rule to Δ OAB,

       E_bph/sinx = E_Rph/sinδ

        So once E_bph is calculated, load angle δ can be determined by using sine rule.

Case ii) Over excitation, E_bph > V_ph

       p.f. is leading in nature.

       E_Rph  ^ I_aph = θ

       V_ph  ^ I_aph = Φ

       The phasor diagram is shown in the Fig. 2.

Fig.2  Phasor diagram for overexcited condition

       Applying cosine rule to Δ OAB,

       (E_bph)² = (V_ph)² + (E_Rph)² - 2V_ph  E_Rph x cos(V_ph ^ E_Rph)

       V_ph ^ E_Rph = θ + Φ

.^..    (E_bph)² = (V_ph)² + (E_Rph)² - 2 V_ph   E_Rph cos(θ + Φ) .......(3)

       But θ + Φ is generally greater than  90^o

.^..    cos (θ + Φ) becomes negative, hence for leading p.f., E_bph > V_ph .

       Applying sine rule to Δ OAB,

       E_bph/sin( E_Rph ^ V_ph) = E_Rph/sinδ

       Hence load angle δ can be calculated once E_bph is known.

Case iii) Critical excitation

       In this case E_{bph ≈} V_ph, but p.f. of synchronous motor is unity.

.^..         cos = 1   .^..    Φ = 0^o

       i.e. V_ph and I_aph are in phase

       and  E_Rph ^ I_aph = θ

       Phasor diagram is shown in the Fig. 3.

Fig. 3  Phasor diagram for unity p.f. condition

       Applying cosine rule to OAB,

       (E_bph)² = (V_ph)² + (E_Rph)² - 2V_ph E_Rph cos θ            ............(5)

       Applying sine rule to OAB,

       E_bph/sinθ = E_Rph/sinδ

       where   E_Rph = I_aph x Zs V