Case i) Under excitation, Ebph < Vph .
Zs = Ra + j Xs = | Zs | ∟θ Ω
θ = tan-1(Xs/Ra)
ERph ^ Iaph = θ, Ia lags always by angle θ.
Vph = Phase voltage applied
ERph = Back e.m.f. induced per phase
ERph = Ia x Zs V ... per phase
Let p.f. be cosΦ, lagging as under excited,
Vph ^ Iaph = Φ
Phasor diagram is shown in the Fig. 1.
 |
| Fig. 1 Phasor diagram for under excited condition |
Applying cosine rule to Δ OAB,
(Ebph)2 = (Vph)2 + (ERph)2 - 2Vph ERph x (Vph ^ ERph)
but Vph ^ ERph = x = θ - Φ
(Ebph)2 = (Vph)2 + (ERph)2 - 2Vph ERph x (θ - Φ) ......(1)
where ERph = Iaph x Zs
Applying sine rule to Δ OAB,
Ebph/sinx = ERph/sinδ
So once Ebph is calculated, load angle δ can be determined by using sine rule.
Case ii) Over excitation, Ebph > Vph
p.f. is leading in nature.
ERph ^ Iaph = θ
Vph ^ Iaph = Φ
The phasor diagram is shown in the Fig. 2.
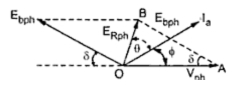 |
| Fig.2 Phasor diagram for overexcited condition |
Applying cosine rule to Δ OAB,
(Ebph)2 = (Vph)2 + (ERph)2 - 2Vph ERph x cos(Vph ^ ERph)
Vph ^ ERph = θ + Φ
... (Ebph)2 = (Vph)2 + (ERph)2 - 2 Vph ERph cos(θ + Φ) .......(3)
But θ + Φ is generally greater than 90o
... cos (θ + Φ) becomes negative, hence for leading p.f., Ebph > Vph .
Applying sine rule to Δ OAB,
Ebph/sin( ERph ^ Vph) = ERph/sinδ
Hence load angle δ can be calculated once Ebph is known.
Case iii) Critical excitation
In this case Ebph ≈ Vph, but p.f. of synchronous motor is unity.
... cos = 1 ... Φ = 0o
i.e. Vph and Iaph are in phase
and ERph ^ Iaph = θ
Phasor diagram is shown in the Fig. 3.
 |
| Fig. 3 Phasor diagram for unity p.f. condition |
Applying cosine rule to OAB,
(Ebph)2 = (Vph)2 + (ERph)2 - 2Vph ERph cos θ ............(5)
Applying sine rule to OAB,
Ebph/sinθ = ERph/sinδ
where ERph = Iaph x Zs V




No comments:
Post a Comment